Depuis le début du XXe siècle, les psychopédagogues et les sociologues étudient les raisons de l’échec scolaire et les conséquences du redoublement. De nombreuses études scientifiques ont été menées à travers le monde, principalement – mais non seulement – dans les pays anglo-saxon. Ces études réfutent toutes les hypothèses qu’il est possible de formuler quant à d’éventuels effets positifs[1].
On peut donc se demander pourquoi, cent ans après les résultats des premières recherches, les enseignants continuent à tenir autant à une pratique pédagogique qui ne sert à rien, qui est contre-productive et génère chez les jeunes qui le subissent une telle souffrance.
Nous pouvons nous interroger sur l’efficacité de la formation initiale mais également sur la pression exercée par les pouvoirs organisateurs, les directions et certaines familles pour que les enseignants maintiennent, par la pratique systématique de la mise en échec des élèves, le niveau ( ?) de l’école.
Nous postulons que si les enseignants, qui sont dans leur immense majorité de vrais citoyens soucieux du bien être de leurs élèves, continuent à pratiquer le redoublement, c’est parce qu’ils n’en connaissent ni l’inutilité, ni les conséquences dramatiques qu’il peut avoir sur le plan psychologique auprès des élèves et de leurs familles. Ils n’ont probablement pas été mis face aux résultats de ces centaines d’études qui, toutes, démontrent que le redoublement est absolument néfaste sur les apprentissages et le vécu des élèves.
Aussi avons-nous repris ci-dessous les résultats de nombreuses recherches sur les effets du redoublement, recensées par le chercheur belge en sciences de l’éducation Marcel Crahay, et parues dans son livre Peut-on lutter contre l’échec scolaire ? (Pour plus d’informations, lire son livre). Celles-ci sont, sans doute, les plus accessibles à un public non familiarisé avec ce type de recherche.
1. SEIBEL (France 1984)
L’étude de Seibel indique clairement que le redoublement ne favorise pas l’évolution pédagogique des élèves. Elle a ceci d’intéressant, qu’elle a comporté le suivi de 1 100 élèves aux épreuves standardisées de français et de mathématique entre juin (CP – 1ère année primaire) et décembre 1983 (CE1 – 2e année primaire)[2].
Parmi les élèves qui ont été promus en 2e année, Seibel identifie plusieurs catégories d’élèves. Ceux qui ont connu l’échec une année auparavant et viennent de réussir en juin sont désignés par l’expression « redoublants anciens ». Parmi ceux qui ont réussi en juin, Seibel distingue encore 3 autres catégories d’élèves : les « forts », les « moyens » et les « faibles », en fonction des résultats du test de juin. L’appellation « redoublants nouveaux » concerne donc les élèves qui ont raté le test de juin et se retrouvent à nouveau dans la même classe.
Résultats aux tests de français entre juin et décembre
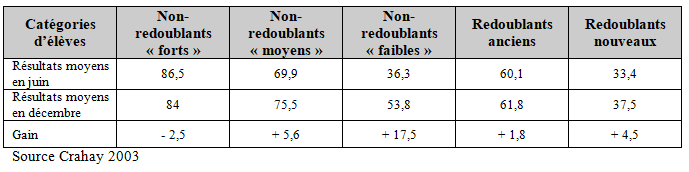
Résultats aux tests de mathématique entre juin et décembre
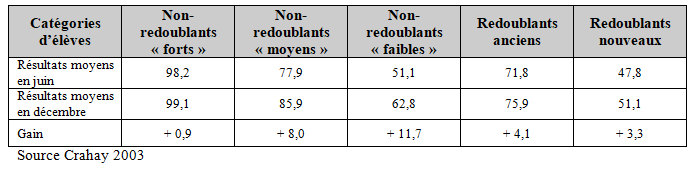
Plusieurs constats s’imposent :
- En juin, les non-redoublants « faibles » et les redoublants nouveaux diffèrent peu (2,9 points en français et 3,3 points en mathématique). Mais quatre mois plus tard, aux tests de décembre, les écarts entre ces groupes se sont fortement creusés (16,3 points en français et 11,7 points en mathématique). La promotion (et donc, le non-redoublement) a été favorable aux élèves « faibles », au contraire des élèves ayant redoublé pour qui le redoublement ne profite pas suffisamment.
- La progression des non-redoublants « faibles » entre juin et décembre est spectaculaire (+ 17,5 points en français et + 11,7 points en mathématique).
- On constate que les redoublants anciens qui, aux tests de juin, obtiennent des scores comparables aux non-redoublants moyens, progressent moins que ceux-ci en décembre (respectivement + 1,8 et + 5,6 en français, et + 8,0 et + 4,1 en mathématique). Siebel conclu qu’on peut y voir un effet à moyen terme du redoublement consenti l’année auparavant.
Ainsi qu’on le voit dans cette étude, le redoublement n’a pas suffisamment profité aux élèves ayant subi un redoublement qui n’obtiennent pas la moyenne en français et à peine en mathématique, contrairement aux élèves qui, tout aussi « faibles », été promus dans la classe supérieure qui obtiennent la moyenne en f rançais et progressent plus encore en mathématique. Le non-redoublement leur a permis de progresser réellement, contrairement à ceux qui ont redoublé.
2. GRISAY (France 1992)
L’étude de Grisay a été menée dans 100 collèges de France et a été constituée de 5 137 élèves entrés en 6e année (1ère secondaire) et qui ont passé les épreuves standardisées de français et de mathématique à la rentrée 90-91. Ils ont été à nouveau testés deux ans plus tard (1992) alors que la majorité d’entre eux se trouvaient en classe de cinquième (2e secondaire). 264 élèves s’étaient vu refuser l’entrée en cinquième. Ces redoublants se trouvaient encore en sixième au moment du post-test. Ils constituent le groupe-cible de l’analyse dont il est question ici.
La corrélation entre la variable redoublement et le critère (les résultats du post-test) est négative (- 0,23). Il en va de même pour le coefficient de régression de cette même variable sur le critère, obtenu sous contrôle des variables de pré-test (- 0,207). Cela signifie qu’à résultats égal aux épreuves de français et de mathématique à leur entrée en 6e, les élèves redoublants obtiennent deux ans plus tard un score de post-test inférieur de plus de deux dixièmes d’écart-type par comparaison avec leurs condisciples non-redoublants.
Cette étude réfute l’hypothèse selon laquelle le redoublement agit comme une remédiation permettant aux élèves de récupérer leurs lacunes et de repartir dans le cursus scolaire avec de meilleurs atouts. Le caractère nocif du redoublement est établi !
3. Holmes et Mattews (Etats-Unis 1984)
Holmes et Mattews ont examiné quarante-quatre recherches portant sur les effets du redoublement. Toutes présentaient suffisamment de garanties quant à la rigueur méthodologique de l’investigation. Le tableau ci-dessous indique la variable-critère considérée, le nombre d’études à partir desquelles l’ampleur de l’effet a été calculée, et l’ampleur de l’effet.
Ampleur de l’effet du redoublement (en fraction d’écart-type) sur une série de variables-critères (adapté de Holmes et Mattews)
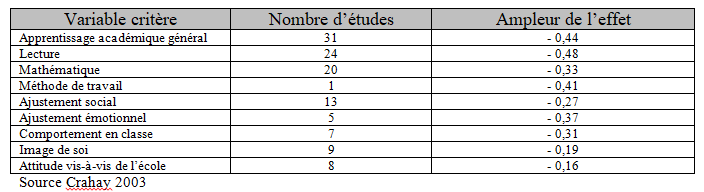
Tous les effets sont négatifs, que le critère d’évaluation soit cognitif ou affectif. Le redoublement est préjudiciable aux élèves qui en font l’objet. L’amplitude de l’effet est proche de – 0,50. Ceci signifie que les élèves redoublants ont, au terme de l’année redoublée, des performances sensiblement moins bonnes que des élèves qui, au départ, avaient le même niveau de compétence, mais ont été promus. Par ailleurs, Holmes et Mattews montrent que ces effets négatifs se retrouvent quelle que soit l’année redoublée.
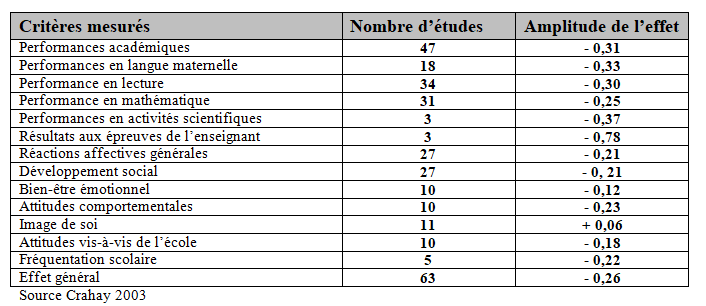
4. Holmes (Etats-Unis 1990)
En 1990, Holmes a mené une étude reprenant 63 recherches dont 44 faisaient partie de sa recherche précédente avec Mattews (1984). Les résultats, ci-dessous, démontrent que tous les effets sont négatifs, à l’exception de l’image de soi (l’effet d’amplitude est négligeable ; les effets inférieurs à 0,15 sont à considérer comme peu ou non significatifs. En outre, une composante psychologique est plus appréhendable par des tests que les acquis cognitifs). On soulignera l’influence négative de cette mesure « pédagogique » sur les gains de connaissance des élèves.
Ampleur de l’effet du redoublement (en fraction d’écart type) sur une série de variables-critères (adapté de Holmes, 1990)
Ampleur de l’effet du redoublement (en fraction de l’écart-type) mesurée par des tests de connaissance en fonction du niveau d’étude auquel survient le redoublement (adapté de Holmes, 1990)

On notera que toutes les valeurs sont négatives. C’est lorsque le redoublement intervient au milieu de la scolarité primaire que les effets sont le moins négatifs (- 0,10 en deuxième primaire et – 0,15 en troisième primaire).
Contrairement à une opinion largement répandue, le redoublement en troisième maternelle n’a aucun effet préventif ou correcteur. Nous verrons plus loin qu’il est, comme tous les redoublements, totalement inutile.
Enfin, le redoublement a des effets plus préjudiciables encore lorsqu’il intervient en fin de scolarité primaire (- 0,38).
5. Holmes (Etats-Unis 1990)
Le principe du redoublement, pour nombre d’enseignants, consiste à sacrifier une année pour permettre à des enfants de repartir sur de meilleures bases et atteindre – avec une année de retard, certes – des niveaux ce compétences auxquels ils auraient pu prétendre s’ils n’avaient pas redoublé.
Si cela devait s’avérer exact, on constaterait que les élèves ayant redoublés auraient de meilleurs résultats que leurs condisciples aussi « faibles » mais qui, eux, ont été promus, et ce à un même niveau scolaire.
Dans quelques-unes des études recensées par Holmes (1990), les élèves redoublants et leurs condisciples « faibles » n’ayant pas redoublés ont été suivis pendant plusieurs années. Ceci permet de se faire une idée de l’effet à moyen terme du redoublement.
Holmes a procédé à deux types de comparaisons :
- Dans un premier cas, il a comparé les élèves « faibles » qui ont redoublé, avec leurs condisciples aussi « faibles » qui n’ont pas redoublé. Ces derniers ont bénéficié des enseignements d’une année complémentaires alors que les premiers recommençaient leur année. Il s’agit d’une comparaison à âge constant.
- Dans un second cas, il a comparé les élèves « faibles » redoublants et « faibles » non-redoublants au terme de la même année scolaire, en sachant que les premiers ont eu un an de plus par rapport aux seconds. Il s’agit d’une comparaison à degré scolaire constant.
Supposons un groupe d’élèves qui est entré en première année primaire en 2004. En fin d’année, une partie d’entre eux a redoublé et une autre partie a été promue. Imaginons que la suite du parcours se réalise sans embûches. Cela conduira à la situation suivante :

Les élèves ont été testés à la fin de chaque année. Voici les résultats obtenus selon les types de comparaison :
Effet à moyen et à long terme du redoublement (mesuré en fraction d’écart type). Résultats des comparaisons à âge constant (adapté de Holmes 1990)

Effet à moyen et à long terme du redoublement (mesuré en fraction d’écart type). Résultats des comparaisons à degré scolaire constant (adapté de Holmes 1990)

Ce double constat est éclairant. Lorsqu’on compare le niveau cognitif atteint par les redoublants et les non-redoublants à même degré scolaire, les performances des uns et des autres sont équivalentes. Et cela reste vrai que les comparaisons soient établies un an après le redoublement ou plus de trois ans après.
Il importe, toutefois, de souligner que les redoublants ont pris une année de plus pour aboutir au même résultat que leurs condisciples qui, tout aussi « faibles » qu’eux, ont eu la chance de tomber sur des enseignants qui les ont promus.
En revanche, lorsqu’on examine la comparaison à âges constants, on observe un retard qui va en s’accroissant avec les années des élèves qui ont redoublé par rapport à ceux qui ont été promus.
Bref, une année redoublée est bien une année perdue puisqu’elle conduit les élèves faibles au niveau qu’ils atteindraient une année plus tôt qu’ils avaient pu poursuivre leur scolarité avec les condisciples de leur âge.
Conclusion
Toutes les études démontrent que le redoublement est inefficace. Au mieux permet-il aux élèves d’évoluer comme ils auraient évolués sans redoubler, mais avec une année de plus. Peut-on, dès lors accepter, que l’Ecole contraignent les enfants à perdre une année de leur vie, et ce pour rien ?
Nous pensons que faire perdre inutilement une ou plusieurs années de vie à un élève est de la maltraitance.


